Comprendre le concept d’identité remarquable en mathématiques

Le concept d'identités remarquables est un outil mathématique important qui peut être utilisé pour résoudre des problèmes complexes. Il est important de comprendre comment fonctionnent ces identités et comment les utiliser de manière efficace. L'identité remarquable est un concept mathématique qui peut être utilisé pour simplifier et résoudre des équations. Ce concept est souvent utilisé par les étudiants en mathématiques, car il peut leur permettre de mieux comprendre et de résoudre des problèmes.

Quelles sont les principales identités remarquables ?

Il existe de nombreuses identités remarquables en mathématiques, mais certaines d'entre elles sont plus connues que d'autres. Parmi les plus célèbres, on peut citer l'identité remarquable de Pythagore, l'identité de Euler et l'identité de Gauss.

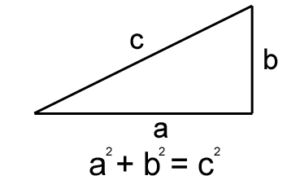
• Le théorème de Pythagore est une relation mathématique qui permet de déterminer la longueur d'un côté d'un triangle rectangle en fonction de la longueur des deux autres côtés. Elle s'écrit de la manière suivante : a^2 + b^2 = c^2.
• L'identité de Euler est une relation mathématique qui établit un lien entre les nombres complexes et les nombres réels. Elle s'écrit de la manière suivante : e^{i\pi} + 1 = 0.
• L'identité de Gauss est une relation mathématique qui permet de calculer la somme des nombres entiers compris entre 1 et un nombre donné n. Elle s'écrit de la manière suivante : \sum_{k=1}^{n} k = \frac{n(n+1)}{2}.

Comment utiliser une identité remarquable ?

Il y a quelques concepts mathématiques qui sont difficiles à comprendre, mais une fois que vous les avez maîtrisés, ils peuvent être très utiles. Les identités remarquables en font partie. Un identité remarquable est une égalité qui est vraie pour tous les nombres dans une certaine plage. Par exemple, l'identité remarquable (a + b)² = a² + 2ab + b² est vraie pour tous les nombres a et b. Cela signifie que si vous avez une expression qui a la forme (a + b)², vous pouvez l'écrire sous la forme a² + 2ab + b². Cela peut vous sembler un peu mystérieux, mais c'est en fait très utile. Supposons que vous deviez calculer (2 + 3)². Vous pouvez utiliser l'identité remarquable pour le faire. (2 + 3)² = 2² + 2*2*3 + 3² = 4 + 12 + 9 = 25. Vous pouvez voir que cela fonctionne pour n'importe quelle valeur de a et b. Il y a beaucoup d'autres identités remarquables que vous pouvez utiliser pour simplifier les expressions mathématiques. Si vous avez du mal à les retenir, essayez de les utiliser souvent pour vous aider à les mémoriser. Une fois que vous les aurez maîtrisées, vous serez en mesure de résoudre des problèmes plus rapidement et plus facilement.

A quel âge apprend on les identités remarquable à l'école ?

Le concept d'identités remarquables en mathématiques est un sujet qui a suscité beaucoup de débats parmi les mathématiciens. Certains soutiennent qu'il est important de l'apprendre dès le collège, car il permet aux élèves de mieux comprendre les concepts fondamentaux de la mathématique. D'autres soutiennent qu'il est inutile d'apprendre les identités remarquables en mathématiques, car elles ne sont pas utilisées dans la vie de tous les jours. A titre d'exemple, voici ce que l'on doit connaître sur les identités remarquables, en classe de seconde :